Neural Networks: How Do They Learn?
Read Time ~ 8 Minutes
In the last article, The Multilayer Perceptron, I went over the structure of the MLP and talked a bit about what each part of the network does. Due to length I had to forego the topic of how neural networks learn but it’s time for a high level overview as almost all neural networks learn using similar techniques.
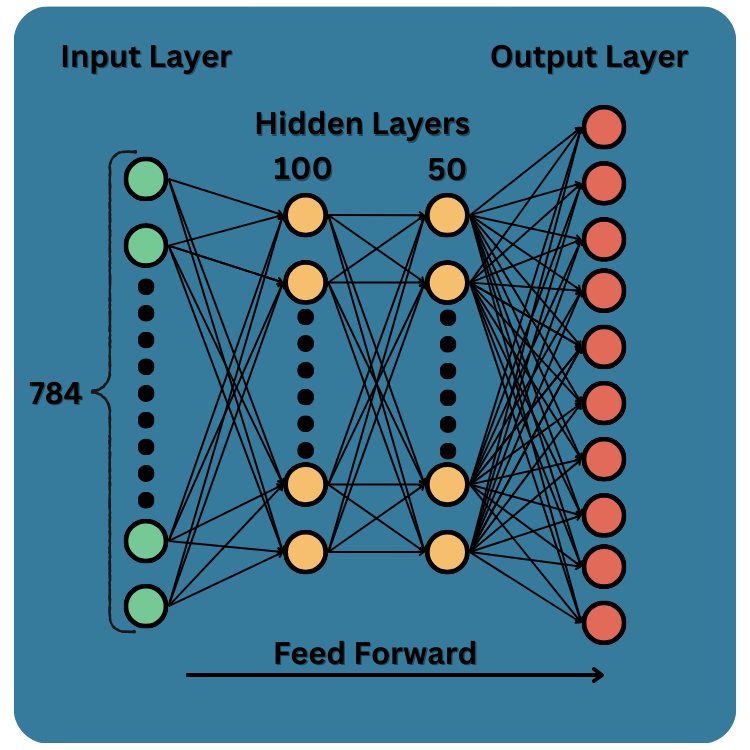
I will use the same example as the last article, the MNIST dataset and a simple MLP. If you haven’t read it yet, I suggest reading that before tackling this if you want a more detailed background of how a MLP works. As a quick overview let’s take a look at the structure of the MLP we set up for the MNIST dataset:
We have an input layer with 784 neurons, one neuron for each pixel of our input image. Two hidden layers one with 100 neurons and another with 50 neurons. Last, an output layer with 10 neurons that correspond with each digit in the MNIST dataset, 0-9.
The goal is, given an image of a handwritten digit, have the network predict which digit it is. Sounds fairly straight forward but how can we make the network learn?
Cost Function
The first step in making the network learn is developing the ability to judge the performance of the network as it makes its predictions. Let’s zoom in on the output layer of the image above and see what the network would look like if it were trying to classify an image of a 4:
As you can see, we have an image of a 4 which has been passed through the network and resulted in the values in the output layer. Each neuron in our output layer corresponds to the different digits in our set of images, 0-9. Each value, which can be between 0 and 1, in each neuron depicts how “confident” the network thinks the input image corresponds to the choices it can be, where 0 is it doesn’t correspond at all and 1 is corresponds completely.
Using this output we can compare it to the ground truth as we know the label of the input image. All we have to do is subtract the ideal output of the network, which in this case the neuron that corresponds to the digit 4 to have a value of 1 and all other neurons to be zero, and our models current predictions. Then we square each result to deal with negative values and add everything together. The resulting number is the “cost” of the network. This number can be thought of how well our model is performing where a smaller cost value is better.
There are many different ways to derive a cost function each with their own strengths and weaknesses. For now, just know that the value of the resulting cost function is a way to judge how well our model is performing.
Gradient Descent
So, we now have a way to quantify how good our model is performing by looking at the cost of our model. We know we want to minimize the cost function but how do we accomplish this?
In a way, the number at the end of our model is a measure that is directly tied to every neuron before it and the way that number was derived was a direct result of every neuron’s associated weights and biases. We also know we can change the weights and biases of our neuron’s in order to effect the value it takes on. Now we need a way to change the weights and biases of a given neuron such that we minimize the cost function. This is where a technique called gradient descent comes into play. Let’s take a look at an example of a simple function, one that can be used as a function within our network:
Technically, the function would be a lot more complex than this but to keep things simple we will use this one.
A function, if you don’t remember, is just something that takes in an input and outputs some other number. In our case that input is a representation of our image’s pixel value and our output is a number that tries to represent that input in a lower dimension/resolution.
So looking at our function we need a way to minimize the value that it outputs. In this example we can actually just look and see that if we input a 3 we will get out a 2, which is the lowest value that our function can output.
However, this method isn’t exactly feasible where we graph the function and visually look where the lowest output is located. If you ever took a calculus class a more mathematical approach would be to take the derivative of the function and see where it is equal to zero. This would correspond to the lowest output of our function…sometimes. See, this works when our function is very simple and has one global minima (lowest point in the function) with no local minima. The functions in our network are rarely so simple. Gradient descent can solve this problem.
With gradient descent we can pick any point on our function and measure it’s derivative. If the slope is not zero and is positive we shift our position to the left, and if our slope is not zero and negative we shift our position to the right. In the picture above we can think of this process as a ball rolling down a hill. In this case the ball is our position on the function and the act of rolling down the hill is the changing of our position due to the derivate at the point. We can do this for every function we encounter in our network to figure out the lowest output our function can take on, at least locally.
Backpropagation
Great, so we have a way to quantify our model as well as adjust the weights and biases within our model. We now need to adjust every weight and bias within our model to minimize our cost function through a process called backpropagation. This isn’t as straight forward as it sounds because of one huge problem.
Let’s say we wanted to adjust the weights and biases on a neuron in the first hidden layer. Due to our network being fully connected, tweaking those values would inherently change the values of every other preceding neuron the follows. This means figuring out what values for our weights and biases are best that minimize the cost function impossible because adjusting one set of them would change every other one.
This is where backpropagation saves the day. We can use a method called the chain rule from calculus that minimizes the cost function with respect to the weights and biases of our whole network all at once. That way every tweak we perform is taken into account as the model is adjusted.
We can do this for each training loop, or epoch, of our model thus teaching it to “learn”.
Wrapping it up
I really tried to forego some of the mathematics behind this topic in favor of a more generalized understanding. If however you would like a more in depth mathematical approach let me know and I would be happy to write a future article cover just that.
I hope you enjoyed this edition of AI insights.
Until next time.
Andrew-
Have something you want me to write about?
Head over to the contact page and drop me a message. I will be more than happy to read it over and see if I can provide any insights!